개요
Tensorflow 공식 가이드의 텐서 소개(Introduction to Tensors)를 정리한 글이며,
모든 이미지의 출처는 위 링크에서 발췌하였다.
텐서Tensor는 텐서플로우와 케라스에서 지원하는 다차원 배열이다.
1
2
import tensorflow as tf
import numpy as np
텐서 객체의 기본적인 특징은 다음과 같다.
-
모든 요소는 같은 자료형(Dtype)을 가진다.
tf.dtypes.DType에서 지원되는 모든 자료형을 확인할 수 있다. -
수정할 수 없다(Immutable).
값의 변경이 필요할 땐 변수(
tf.Variable) 객체를 대신 사용한다. -
넘파이 어레이(
np.array)와 조작 방법이 유사하다.
형상
텐서 객체가 가지고 있는 형태를 형상Shape이라 한다.
형상을 설명하기 위한 예제로 4D 텐서를 생성한다.
1
rank_4_tensor = tf.zeros([3, 2, 4, 5])
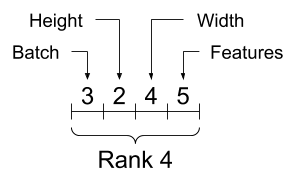
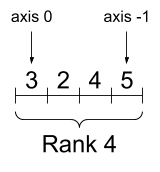
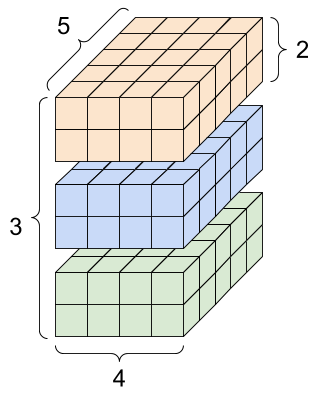
생성한 4D 텐서를 시각화하면 다음과 같다.
-
형상Shape
텐서의 각 차원의 길이를 의미한다.
Shape=(3, 2, 4, 5)
-
차원Rank
텐서의 축의 수를 의미한다.
축이 총 4개(3, 2, 4, 5)이므로 Rank=4
-
축Axis
텐서의 특정 차원을 의미한다.
axis를 사용해 각 축에 접근할 수 있다.
Note 텐서를 구성하는 일반적인 축 순서는 배치 -> 차원 -> 특성 순이다.
-
크기Size
텐서의 총 항목의 곱을 의미한다.
Size = 3 x 2 x 4 x 5 = 120
다음과 같이 텐서 객체의 속성을 통해 형상 정보에 접근할 수 있다.
1
2
3
4
5
6
print("Type of every element:", rank_4_tensor.dtype) # 자료형
print("Number of dimensions:", rank_4_tensor.ndim) # 차원
print("Shape of tensor:", rank_4_tensor.shape) # 형상
print("Elements along axis 0 of tensor:", rank_4_tensor.shape[0]) # axis=0의 요소 수
print("Elements along the last axis of tensor:", rank_4_tensor.shape[-1]) # axis=-1의 요소 수
print("Total number of elements (3*2*4*5): ", tf.size(rank_4_tensor).numpy()) # 크기
1
2
3
4
5
6
Type of every element: <dtype: 'float32'>
Number of dimensions: 4
Shape of tensor: (3, 2, 4, 5)
Elements along axis 0 of tensor: 3
Elements along the last axis of tensor: 5
Total number of elements (3*2*4*5): 120
텐서 생성
텐서 객체의 형상은 일반적으로 직사각형 모양이며, 이를 정형 텐서라 한다.
정형 텐서는 각 축을 따라 모든 요소의 크기가 같다.
반면 그렇지 않은 텐서도 존재하며, 이를 비정형 텐서라 한다.
텐서를 구성하는 요소가 대부분이 비어 있어 데이터가 희소한 경우를 희소 텐서라 한다.
(비정형 텐서 및 희소 텐서는 후술)
정형 텐서는 tf.constant() 함수를 사용해 생성한다.
value로 단일 값을 사용하면 0차원 텐서를 생성하며, dtype 매개변수로 텐서의 자료형을 지정한다.
매개변수를 직접 지정하지 않으면 Python의 정수를 tf.int32로, Python의 부동 소수점을 tf.float32로 자동 변환한다.
0차원 텐서는 스칼라Scalar라 한다.
1
2
3
4
# Rank=0 (Scalar)
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
1
tf.Tensor(4, shape=(), dtype=int32)
value로 리스트를 사용하면 더 높은 차원의 텐서를 생성할 수 있다.
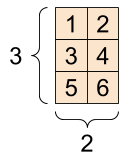
1차원 텐서는 벡터Vector, 2차원 텐서는 행렬Matrix이라 한다.
이미지 등의 데이터를 저장하는 텐서는 3개 이상의 축을 가지기도 한다.
이러한 텐서를 다차원 텐서라고 하며, 주로 nD 텐서(n은 텐서의 차원)로 표현한다.
| 스칼라 | 벡터 | 행렬 | 3차원 이상의 텐서 |
|---|---|---|---|
 |
 |
 |
 |
1
2
3
4
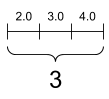
# Rank=1 (Vector)
rank_1_tensor = tf.constant([2., 3., 4.])
print(rank_1_tensor)
1
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
1
2
3
4
5
6
# Rank=2 (Matrix)
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)
1
2
3
4
tf.Tensor(
[[1. 2.]
[3. 4.]
[5. 6.]], shape=(3, 2), dtype=float16)
1
2
3
4
5
6
7
8
9
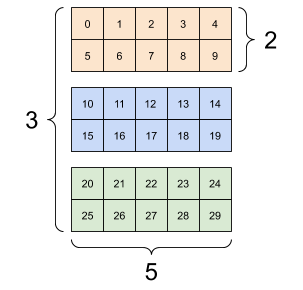
# Rank=3
rank_3_tensor = tf.constant([[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]],])
print(rank_3_tensor)
1
2
3
4
5
6
7
8
9
tf.Tensor(
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]
[[20 21 22 23 24]
[25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
tf.constant() 외에도 다양한 방법으로 텐서를 생성할 수 있다.
예를 들어, tf.ones() 함수는 shape이 주어지면 모든 요소가 1인 텐서를 반환한다.
1
2
3
ones_tensor = tf.ones([2, 3])
print(ones_tensor)
텐서 연산
1
2
3
4
a = tf.constant([[1, 2],
[3, 4]])
b = tf.constant([[1, 1],
[1, 1]])
두 텐서의 모양이 산술 연산의 조건을 만족한다면, 다음과 같은 기본 산술을 수행할 수 있다.
-
덧셈
두 텐서에서 대응하는 요소의 합들로 구성된 텐서를 반환한다.
tf.add(a, b)함수 또는+연산자 사용
1
2
print(tf.add(a, b), '\n')
print(a + b, '\n')
1
2
3
4
5
6
7
tf.Tensor(
[[2 3]
[4 5]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[2 3]
[4 5]], shape=(2, 2), dtype=int32)
-
스칼라 곱
두 텐서에서 대응하는 요소의 곱들로 구성된 텐서를 반환한다.
tf.multiply(a, b)함수 또는*연산자 사용
1
2
print(tf.multiply(a, b), '\n')
print(a * b, '\n')
-
행렬곱
tf.matmul(a, b)함수 또는@연산자 사용
1
2
print(tf.matmul(a, b), "\n")
print(a @ b, "\n")
1
2
3
4
5
6
7
tf.Tensor(
[[3 3]
[7 7]], shape=(2, 2), dtype=int32)
tf.Tensor(
[[3 3]
[7 7]], shape=(2, 2), dtype=int32)
이 외에도 tf에서 제공하는 다양한 함수를 텐서에 적용할 수 있다.
1
2
3
4
5
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
print(tf.reduce_max(c)) # 가장 큰 값
print(tf.argmax(c)) # 가장 큰 인덱스
print(tf.nn.softmax(c)) # 소프트맥스 변환
1
2
3
4
5
tf.Tensor(10.0, shape=(), dtype=float32)
tf.Tensor([1 0], shape=(2,), dtype=int64)
tf.Tensor(
[[2.6894143e-01 7.3105860e-01]
[9.9987662e-01 1.2339458e-04]], shape=(2, 2), dtype=float32)
텐서 인덱싱
파이썬 리스트 및 넘파이 어레이의 인덱싱 규칙과 유사하다.
- 인덱스는 0에서 시작한다.
- 인덱스가 음수인 경우 끝에서부터 거꾸로 계산한다(-1부터 시작).
- 슬라이싱을 지원한다(
start:stop및start:stop:step).
1
2
rank_1_tensor = tf.constant([0, 1, 1, 2, 3, 5, 8, 13, 21, 34])
print(rank_1_tensor.numpy())
1
[ 0 1 1 2 3 5 8 13 21 34]
직관적인 출력 형식을 위해 .numpy() 메서드를 사용해 텐서 객체를 넘파이 어레이로 변환한다.
1
2
3
print("First:", rank_1_tensor[0].numpy())
print("Second:", rank_1_tensor[1].numpy())
print("Last:", rank_1_tensor[-1].numpy())
1
2
3
First: 0
Second: 1
Last: 34
인덱스로 스칼라를 사용하면 축이 제거된다.
축을 유지하려면 슬라이스(:)를 대신 사용한다.
1
2
3
4
5
6
print("Everything:", rank_1_tensor[:].numpy())
print("Before 4:", rank_1_tensor[:4].numpy())
print("From 4 to the end:", rank_1_tensor[4:].numpy())
print("From 2, before 7:", rank_1_tensor[2:7].numpy())
print("Every other item:", rank_1_tensor[::2].numpy())
print("Reversed:", rank_1_tensor[::-1].numpy())
1
2
3
4
5
6
Everything: [ 0 1 1 2 3 5 8 13 21 34]
Before 4: [0 1 1 2]
From 4 to the end: [ 3 5 8 13 21 34]
From 2, before 7: [1 2 3 5 8]
Every other item: [ 0 1 3 8 21]
Reversed: [34 21 13 8 5 3 2 1 1 0]
2차원 텐서의 경우 두 개의 인덱스를 사용해 인덱싱한다.
1
print(rank_2_tensor.numpy())
1
2
3
[[1. 2.]
[3. 4.]
[5. 6.]]
1
print(rank_2_tensor[1, 1].numpy())
1
4.0
1
2
3
4
5
6
print("Second row:", rank_2_tensor[1, :].numpy())
print("Second column:", rank_2_tensor[:, 1].numpy())
print("Last row:", rank_2_tensor[-1, :].numpy())
print("First item in last column:", rank_2_tensor[0, -1].numpy())
print("Skip the first row:")
print(rank_2_tensor[1:, :].numpy())
1
2
3
4
5
6
7
Second row: [3. 4.]
Second column: [2. 4. 6.]
Last row: [5. 6.]
First item in last column: 2.0
Skip the first row:
[[3. 4.]
[5. 6.]]
형상 조작
텐서 객체는 앞서 언급했듯 불변(Immutable)이다.
따라서 형상 조작을 위해서는 먼저 tf.Variable() 함수를 사용해 변수로 변환해야 한다.
1
2
3
var_x = tf.Variable(tf.constant([[1], [2], [3]]))
print(var_x.shape)
1
(3, 1)
1
print(var_x.shape.as_list())
1
[3, 1]
1
2
3
4
5
# 형상이 변환된 새 텐서 reshaped를 생성한다.
reshaped = tf.reshape(var_x, [1, 3])
print(var_x.shape)
print(reshaped.shape)
1
2
(3, 1)
(1, 3)
텐서를 평탄화하면, 텐서를 구성하는 요소의 메모리 순서를 알 수 있다.
설명을 위해 앞서 생성했던 3D 텐서를 사용한다.
1
print(rank_3_tensor)
1
2
3
4
5
6
7
8
9
tf.Tensor(
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]
[[20 21 22 23 24]
[25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
Tensorflow는 행 중심 메모리 순서를 사용하므로 다음과 같은 결과가 출력된다.
1
print(tf.reshape(rank_3_tensor, [-1]))
1
2
3
tf.Tensor(
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29], shape=(30,), dtype=int32)
tf.reshape() 함수를 사용하면 다양한 형상으로의 변환이 가능하다.
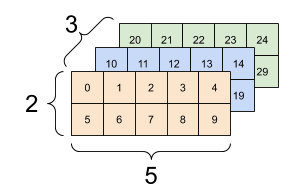
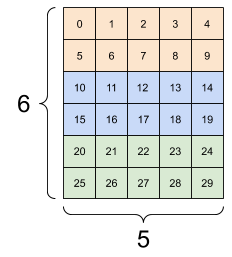
다음은 기존의 3x2x5 텐서를 3x(2x5) 또는 (3x2)x5 텐서로 변환한 예시이다.
| 3x2x5 | 3x10 | 6x5 |
|---|---|---|
 |
 |
 |
1
2
print(tf.reshape(rank_3_tensor, [3*2, 5]), "\n")
print(tf.reshape(rank_3_tensor, [3, -1]))
1
2
3
4
5
6
7
8
9
10
11
12
tf.Tensor(
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]
[20 21 22 23 24]
[25 26 27 28 29]], shape=(6, 5), dtype=int32)
tf.Tensor(
[[ 0 1 2 3 4 5 6 7 8 9]
[10 11 12 13 14 15 16 17 18 19]
[20 21 22 23 24 25 26 27 28 29]], shape=(3, 10), dtype=int32)
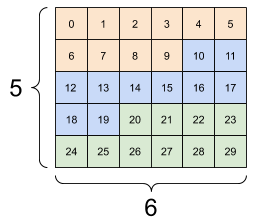
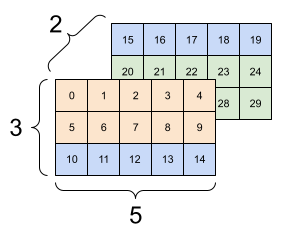
그러나 축의 순서를 고려하지 않는다면, 텐서의 형상 변환은 큰 의미를 가지지 않는다.
다음은 형상 변환의 잘못된 예시이다.
| 5x6 | 2x3x5 | ?x7 |
|---|---|---|
 |
 |
 |
형상 변환의 결과는 정형 텐서여만 한다. 3번 그림과 같은 변환은 오류를 발생시킨다.
브로드캐스팅
차원이 다른 두 텐서 간 연산에서, 특정 조건을 만족할 때 작은 텐서가 큰 텐서에 맞게 자동으로 확장되는 것을 브로드캐스팅Broadcasting이라 한다.
텐서와 스칼라의 곱을 예시로 들 수 있다.
1
2
3
x = tf.constant([1, 2, 3])
y = tf.constant(2)
z = tf.constant([2, 2, 2])
벡터 x에 스칼라 2를 곱하거나, 모든 요소가 2인 같은 크기의 벡터 z를 곱하거나, 그 결과는 같다.
1
2
3
print(tf.multiply(x, 2))
print(x * y)
print(x * z)
1
2
3
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)
다음과 같이 3x1 벡터와 1x4 벡터를 행렬곱하는 경우, 3x4 행렬을 반환한다.
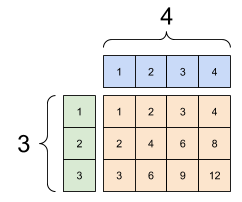
1
2
3
4
5
6
x = tf.reshape(x,[3,1])
y = tf.range(1, 5)
print(x, "\n")
print(y, "\n")
print(tf.multiply(x, y))
1
2
3
4
5
6
7
8
9
10
11
tf.Tensor(
[[1]
[2]
[3]], shape=(3, 1), dtype=int32)
tf.Tensor([1 2 3 4], shape=(4,), dtype=int32)
tf.Tensor(
[[ 1 2 3 4]
[ 2 4 6 8]
[ 3 6 9 12]], shape=(3, 4), dtype=int32)
브로드캐스팅 과정은 다음과 같은 형태로 확장하는 과정을 거치지 않으므로 메모리를 효율적으로 사용한다.
1
2
3
4
5
6
7
8
9
x_stretch = tf.constant([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
y_stretch = tf.constant([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
print(x_stretch * y_stretch)
1
2
3
4
tf.Tensor(
[[ 1 2 3 4]
[ 2 4 6 8]
[ 3 6 9 12]], shape=(3, 4), dtype=int32)
텐서가 브로드캐스팅된 모습은 tf.broadcast_to 함수를 사용해 확인할 수 있다.
1
print(tf.broadcast_to(tf.constant([1, 2, 3]), [3, 3]))
1
2
3
4
tf.Tensor(
[[1 2 3]
[1 2 3]
[1 2 3]], shape=(3, 3), dtype=int32)
문자열 텐서
tf.string은 텐서 자료형 중 하나로, 문자열 데이터를 표현한다.
이를 요소로 하는 텐서를 문자열 텐서라 한다.
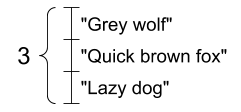
문자열의 길이는 텐서의 축이 아니다. 따라서 위 텐서는 모양이 (3, )인 벡터이다.
1
2
3
4
5
tensor_of_strings = tf.constant(["Gray wolf",
"Quick brown fox",
"Lazy dog"])
print(tensor_of_strings)
1
tf.Tensor([b'Gray wolf' b'Quick brown fox' b'Lazy dog'], shape=(3,), dtype=string)
위 출력에서 각 문자열의 앞에 b 접두사가 붙은 것을 확인할 수 있다.
이는 tf.string이 유니코드 문자열이 아닌, 바이트 문자열임을 의미한다.
유니코드 문자열을 입력하면 UTF-8로 인코딩되는 것에 주의해야 한다.
1
tf.constant("🥳👍")
1
<tf.Tensor: shape=(), dtype=string, numpy=b'\xf0\x9f\xa5\xb3\xf0\x9f\x91\x8d'>
tf.strings.split을 사용하면 특정 문자를 구분자로 하여, 다음과 같이 문자열 텐서를 비정형 텐서로 분할할 수 있다.

1
print(tf.strings.split(tensor_of_strings, sep=" "))
1
<tf.RaggedTensor [[b'Gray', b'wolf'], [b'Quick', b'brown', b'fox'], [b'Lazy', b'dog']]>
비정형 텐서
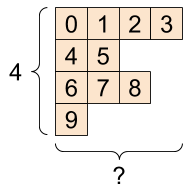
정형 텐서와는 달리, 어떤 축을 따라 요소의 크기가 다양한 텐서를 비정형 텐서라 한다.
비정형 텐서는 tf.ragged.constant() 함수를 사용해 생성한다.
1
2
3
4
5
ragged_list = [
[0, 1, 2, 3],
[4, 5],
[6, 7, 8],
[9]]
1
2
3
ragged_tensor = tf.ragged.constant(ragged_list)
print(ragged_tensor)
1
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>
요소의 크기가 다양한 축의 길이는 None으로 출력된다.
1
print(ragged_tensor.shape)
1
(4, None)
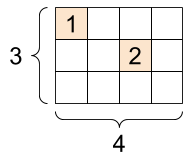
희소 텐서
텐서를 구성하는 요소가 대부분이 비어 있는 경우, 일반적인 방법으로 생성한 텐서 객체는 메모리-비효율적이다.
희소 텐서는 데이터의 인덱스를 저장하는 방식으로 이러한 문제를 해결한다.
1
2
3
4
5
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]],
values=[1, 2],
dense_shape=[3, 4])
print(sparse_tensor)
1
2
3
SparseTensor(indices=tf.Tensor(
[[0 0]
[1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))
다음 코드는 희소 텐서를 평범한 텐서로 변환해 출력한다.
1
print(tf.sparse.to_dense(sparse_tensor))
1
2
3
4
tf.Tensor(
[[1 0 0 0]
[0 0 2 0]
[0 0 0 0]], shape=(3, 4), dtype=int32)