그래프 이론
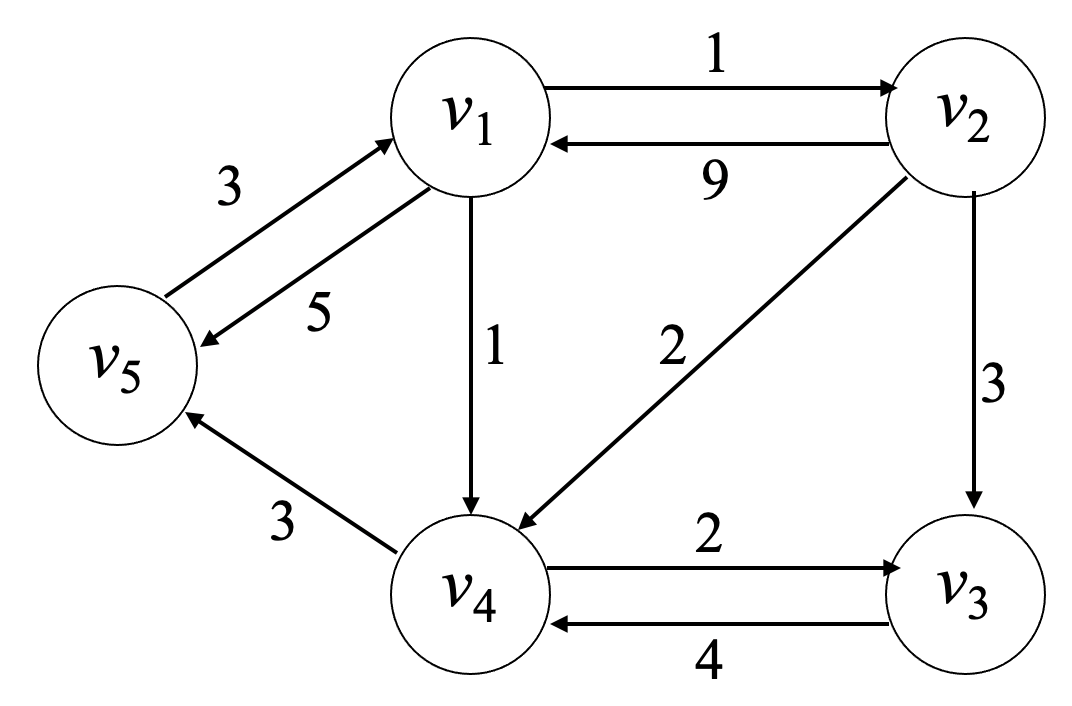
✒ 이미지 출처: https://codingalzi.github.io/algopy/notebooks/algopy06_Dynamic_Programming_2.html
그래프는 정점(vertex)과 정점들을 연결하는 이음선(edge)으로 구성된다.
각각의 이음선이 가중치(weight)를 갖는 그래프를 가중 그래프(weighted graph), 그렇지 않은 그래프를 비가중 그래프(unweighted graph)라고 한다.
각각의 이음선이 방향(direction)을 갖는 그래프를 유향 그래프(directed graph; digraph), 그렇지 않은 그래프를 무향 그래프(undirected graph)라고 한다.
그래프의 경로(path)는 한 정점에서 다른 정점으로 가는 이음선들의 모음이며, 경로의 길이(length)가 최소가 되는 경로를 최단 경로라고 한다.
| 그래프 종류 | 경로의 길이 |
|---|---|
| 가중 그래프 | 경로 상에 있는 가중치의 합 |
| 비가중 그래프 | 경로 상에 있는 이음선의 수 |
비가중 그래프
정의
Edge와 Graph 클래스를 정의하고, TypeVar을 사용해 정접 타입을 선언한다.
| 속성 | 타입 |
|---|---|
| 그래프 | Graph |
| 정점 | V |
| 이음선 | Edge |
edge.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from __future__ import annotations
from dataclasses import dataclass
@dataclass # __init__ 자동 생성
class Edge:
u:int # 정점(from)
v:int # 정점(to)
def reversed(self) -> Edge:
return Edge(self.v, self.u)
def __repr__(self) -> str:
return f"{self.u} -> {self.v}"

Edge 클래스는 두 개의 정점으로 구성되어 있다.
Note
dataclass 모듈의 @dataclass 데코레이터를 사용하면은 특수 메서드를 사용자 정의 클래스에 자동으로 추가할 수 있다. 데코레이터의 매개변수의 기본값은 다음과 같다.
init = True
__init__() 특수 메서드를 생성한다. 이미 정의했다면 이 매개변수는 무시된다.
repr = True
__repr__() 특수 메서드를 생성한다. 이미 정의했다면 이 매개변수는 무시된다.
eq = True
__eq__() 특수 메서드를 생성한다. 이미 정의했다면 이 매개변수는 무시된다.
order = True
__lt__() __le__() __gt__() __ge__()특수 메서드를 생성한다. 이미 정의했다면 TypeError가 발생하며, order가 참이고 eq가 거짓이면 ValueError가 발생한다.
✒ Ref: https://docs.python.org/ko/3/library/dataclasses.html
graph.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from typing import TypeVar, Generic, List, Optional
from edge import Edge
V = TypeVar("V") # 그래프 정점(vertice) 타입
class Graph(Generic[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[Edge]] = [[] for _ in vertices]
@property
def vertex_count(self) -> int:
return len(self._vertices) # 반환: 정점의 수
@property
def edge_count(self) -> int:
return sum(map(len, self._edges)) # 반환: Edge의 수
# map 함수를 통해 _edges 리스트의 각 항목의 길이를 구한 뒤, sum 함수를 사용해 모두 합친다.
def add_vertex(self, vertex:V) -> int:
self._vertices.append(vertex)
self._edges.append([])
return self.vertex_count - 1 # 반환: 정점의 인덱스
# Edge 추가
def add_edge(self, edge:Edge) -> None:
self._edges[edge.u].append(edge)
self._edges[edge.v].append(edge.reversed())
# 정점 a: a -> b
# 정점 b: b -> a
# 정점 인덱스를 사용하여 Edge 추가
def add_edge_by_indices(self, u:int, v:int) -> None:
edge:Edge = Edge(u, v)
self.add_edge(edge)
# 정점 인덱스를 참조하여 Edge 추가
def add_edge_by_vertices(self, first:V, second:V) -> None:
u:int = self._vertices.index(first)
v:int = self._vertices.index(second)
self.add_edge_by_indices(u, v)
# index 함수를 사용하면 위치를 찾을 수 있다.
# 인덱스 -> 정점
def vertex_at(self, index:int) -> V:
return self._vertices[index]
# 정점 -> 인덱스
def index_of(self, vertex:V) -> int:
return self._vertices.index(vertex)
# 정점 인덱스에 연결된 정점
def neighbors_for_index(self, index:int) -> List[V]:
return list(map(self.vertex_at, [e.v for e in self._edges[index]]))
# 엣지의 모든 끝 점(v)의 각 인덱스에 해당하는 정점의 리스트
# 정점에 연결된 이웃 정점
def neighbors_for_vertex(self, vertex:V) -> List[V]:
return self.neighbors_for_index(self.index_of(vertex))
# 정점 인덱스에 연결된 Edge
def edges_for_index(self, index:int) -> List[Edge]:
return self._edges[index]
# 정점에 연결된 Edge
def edges_for_vertex(self, vertex:V) -> List[Edge]:
return self.edges_for_index(self.index_of(vertex))
# 그래프 출력
def __repr__(self) -> str:
desc:str = ""
for i in range(self.vertex_count):
desc += f"{self.vertex_at(i)} -> {self.neighbors_for_index(i)}\n"
return desc

Graph 클래스는 여러 정점(vertices)과 여러 이음선(edges)으로 구성되어 있다. 그래프의 모든 정점을 항목으로 갖는 리스트(self._vertices:List[V])와, 모든 이음선을 항목으로 갖는 리스트(self._edges:List[List[Edge]])를 작성한다. 두 리스트는 동일한 인덱스 규칙을 갖는다. self._index 리스트의 x번째 항목은 x번째 정점에서 출발하는 edge로 구성되어 있다.
정점 정보 입력은 Graph 객체를 생성할 때 이루어지는 반면, 이음선 정보 입력은 add_edge 메서드를 통해 이루어진다. add_edge 메서드의 매개변수로 Edge 객체를 일일이 입력하는 과정은 번거로우므로, 헬퍼 메서드를 사용해 정점 인덱스 또는 정점 이름을 통해 입력받는다.
출력
정점으로 str 타입을 사용한다.
graph.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
if __name__ == "__main__":
city_graph:Graph[str] = Graph(
["시애틀" , "샌프란시스코", "로스앤젤레스",
"리버사이드" , "피닉스" , "시카고",
"보스턴" , "뉴욕" , "애틀랜타",
"마이애미" , "댈러스" , "휴스턴",
"디트로이트" , "필라델피아" , "워싱턴"])
city_graph.add_edge_by_vertices("시애틀" , "시카고")
city_graph.add_edge_by_vertices("시애틀" , "샌프란시스코")
city_graph.add_edge_by_vertices("샌프란시스코", "리버사이드")
city_graph.add_edge_by_vertices("샌프란시스코", "로스앤젤레스")
city_graph.add_edge_by_vertices("로스앤젤레스", "리버사이드")
city_graph.add_edge_by_vertices("로스앤젤레스", "피닉스")
city_graph.add_edge_by_vertices("리버사이드" , "피닉스")
city_graph.add_edge_by_vertices("리버사이드" , "시카고")
city_graph.add_edge_by_vertices("피닉스" , "댈러스")
city_graph.add_edge_by_vertices("피닉스" , "휴스턴")
city_graph.add_edge_by_vertices("댈러스" , "시카고")
city_graph.add_edge_by_vertices("댈러스" , "애틀랜타")
city_graph.add_edge_by_vertices("댈러스" , "휴스턴")
city_graph.add_edge_by_vertices("휴스턴" , "애틀랜타")
city_graph.add_edge_by_vertices("휴스턴" , "마이애미")
city_graph.add_edge_by_vertices("애틀랜타" , "시카고")
city_graph.add_edge_by_vertices("애틀랜타" , "워싱턴")
city_graph.add_edge_by_vertices("애틀랜타" , "마이애미")
city_graph.add_edge_by_vertices("마이애미" , "워싱턴")
city_graph.add_edge_by_vertices("시카고" , "디트로이트")
city_graph.add_edge_by_vertices("디트로이트" , "보스턴")
city_graph.add_edge_by_vertices("디트로이트" , "워싱턴")
city_graph.add_edge_by_vertices("디트로이트" , "뉴욕")
city_graph.add_edge_by_vertices("보스턴" , "뉴욕")
city_graph.add_edge_by_vertices("뉴욕" , "필라델피아")
city_graph.add_edge_by_vertices("필라델피아" , "워싱턴")
print(city_graph)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
시애틀 -> ['시카고', '샌프란시스코']
샌프란시스코 -> ['시애틀', '리버사이드', '로스앤젤레스']
로스앤젤레스 -> ['샌프란시스코', '리버사이드', '피닉스']
리버사이드 -> ['샌프란시스코', '로스앤젤레스', '피닉스', '시카고']
피닉스 -> ['로스앤젤레스', '리버사이드', '댈러스', '휴스턴']
시카고 -> ['시애틀', '리버사이드', '댈러스', '애틀랜타', '디트로이트']
보스턴 -> ['디트로이트', '뉴욕']
뉴욕 -> ['디트로이트', '보스턴', '필라델피아']
애틀랜타 -> ['댈러스', '휴스턴', '시카고', '워싱턴', '마이애미']
마이애미 -> ['휴스턴', '애틀랜타', '워싱턴']
댈러스 -> ['피닉스', '시카고', '애틀랜타', '휴스턴']
휴스턴 -> ['피닉스', '댈러스', '애틀랜타', '마이애미']
디트로이트 -> ['시카고', '보스턴', '워싱턴', '뉴욕']
필라델피아 -> ['뉴욕', '워싱턴']
워싱턴 -> ['애틀랜타', '마이애미', '디트로이트', '필라델피아']
최단 경로
Graph 클래스는 비가중 그래프이므로 이음선의 수가 최소가 되는 경로를 찾는다. 이는 2장에서 학습했던 너비 우선 탐색을 재사용해 구할 수 있다.
goal_test는 lambda를, successors는 Graph 클래스의 neighbors_for_vertex 메서드를 사용해 구현한다.
| 매개변수 | 인자 | 설명 |
|---|---|---|
initial:T |
root | 시작 지점 |
goal_test:Callable[[T], bool] |
lambda x: x == goal | 목표 지점 |
successors:Callable[[T], List[T]] |
city_graph.neighbors_for_vertex | 다음 지점 |
bfs 함수에 적절한 매개변수를 입력한 뒤, node_to_path 함수를 통해 반환값을 리스트로 변환하고 출력한다.
graph.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
if __name__ == "__main__":
from generic_search import bfs, Node, node_to_path
root = "보스턴"
goal = "마이애미"
bfs_result:Optional[Node[V]] = bfs(root,
lambda x: x == goal,
city_graph.neighbors_for_vertex)
if bfs_result is None:
print("너비 우선 탐색으로 답을 찾을 수 없습니다!")
else:
path:List[V] = node_to_path(bfs_result)
print(f"{root}에서 {goal}까지 최단 경로: ")
print(path)
1
2
보스턴에서 마이애미까지 최단 경로:
['보스턴', '디트로이트', '워싱턴', '마이애미']
Note
상위 디렉터리의 패키지에 접근하기 위해서는 sys 모듈을 사용해 다음과 같이 import한다.
가중 그래프
재정의
기존의 Edge와 Graph 클래스를 재정의하고, 가중치 속성을 추가한다.
| 속성 | 타입 |
|---|---|
| 그래프 | WeightedGraph |
| 정점 | V |
| 이음선 | WeightedEdge |
| 가중치 | float |
weighted_edge.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from __future__ import annotations
from dataclasses import dataclass
from edge import Edge
@dataclass
class WeightedEdge(Edge):
weight:float
def reversed(self) -> WeightedEdge:
return WeightedEdge(self.v, self.u, self.weight)
def __lt__(self, other:WeightedEdge) -> bool:
return self.weight < other.weight
def __repr__(self) -> str:
return f"{self.u} {self.weight} -> {self.v}"
가중치 매개변수를 추가로 가지므로 기존 메서드들을 재정의해 인자 조건을 만족시킨다. 또한 __lt__() 특수 메서드를 구현해 두 이음선의 가중치를 비교하는 기능을 추가한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from typing import TypeVar, Generic, List, Tuple
from graph import Graph
from weighted_edge import WeightedEdge
V = TypeVar("V") # 그래프 정점(vertice) 타입
class WeightedGraph(Generic[V], Graph[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[WeightedEdge]] = [[] for _ in vertices]
def add_edge_by_indices(self, u:int, v:int, weight:float) -> None:
edge:WeightedEdge = WeightedEdge(u, v, weight)
self.add_edge(edge)
def add_edge_by_vertices(self, first:V, second:V, weight:float) -> None:
u:int = self._vertices.index(first)
v:int = self._vertices.index(second)
self.add_edge_by_indices(u, v, weight)
def neighbors_for_index_with_weights(self, index:int) -> List[Tuple[V, float]]:
distance_tuples:List[Tuple[V, float]] = []
for edge in self.edges_for_index(index):
distance_tuples.append((self.vertex_at(edge.v), edge.weight))
return distance_tuples
def __repr__(self) -> str:
desc:str = ""
for i in range(self.vertex_count):
desc += f"{self.vertex_at(i)} -> {self.neighbors_for_index_with_weights(i)}\n"
return desc
Edge 대신 WeightedEdge를 사용하므로 기존 메서드들을 재정의해 인자 조건을 만족시킨다.
출력
가중치 인자를 추가로 입력한다.
weighted_graph.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
if __name__ == "__main__":
city_graph2:WeightedGraph[str] = WeightedGraph(
["시애틀" , "샌프란시스코", "로스앤젤레스",
"리버사이드" , "피닉스" , "시카고",
"보스턴" , "뉴욕" , "애틀랜타",
"마이애미" , "댈러스" , "휴스턴",
"디트로이트" , "필라델피아" , "워싱턴"])
city_graph2.add_edge_by_vertices("시애틀" , "시카고" , 1737)
city_graph2.add_edge_by_vertices("시애틀" , "샌프란시스코", 678)
city_graph2.add_edge_by_vertices("샌프란시스코", "리버사이드" , 386)
city_graph2.add_edge_by_vertices("샌프란시스코", "로스앤젤레스", 348)
city_graph2.add_edge_by_vertices("로스앤젤레스", "리버사이드" , 50)
city_graph2.add_edge_by_vertices("로스앤젤레스", "피닉스" , 357)
city_graph2.add_edge_by_vertices("리버사이드" , "피닉스" , 307)
city_graph2.add_edge_by_vertices("리버사이드" , "시카고" , 1704)
city_graph2.add_edge_by_vertices("피닉스" , "댈러스" , 887)
city_graph2.add_edge_by_vertices("피닉스" , "휴스턴" , 1015)
city_graph2.add_edge_by_vertices("댈러스" , "시카고" , 805)
city_graph2.add_edge_by_vertices("댈러스" , "애틀랜타" , 721)
city_graph2.add_edge_by_vertices("댈러스" , "휴스턴" , 225)
city_graph2.add_edge_by_vertices("휴스턴" , "애틀랜타" , 702)
city_graph2.add_edge_by_vertices("휴스턴" , "마이애미" , 968)
city_graph2.add_edge_by_vertices("애틀랜타" , "시카고" , 588)
city_graph2.add_edge_by_vertices("애틀랜타" , "워싱턴" , 543)
city_graph2.add_edge_by_vertices("애틀랜타" , "마이애미" , 604)
city_graph2.add_edge_by_vertices("마이애미" , "워싱턴" , 923)
city_graph2.add_edge_by_vertices("시카고" , "디트로이트" , 238)
city_graph2.add_edge_by_vertices("디트로이트" , "보스턴" , 613)
city_graph2.add_edge_by_vertices("디트로이트" , "워싱턴" , 396)
city_graph2.add_edge_by_vertices("디트로이트" , "뉴욕" , 482)
city_graph2.add_edge_by_vertices("보스턴" , "뉴욕" , 190)
city_graph2.add_edge_by_vertices("뉴욕" , "필라델피아" , 81)
city_graph2.add_edge_by_vertices("필라델피아" , "워싱턴" , 123)
print(city_graph2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
시애틀 -> [('시카고', 1737), ('샌프란시스코', 678)]
샌프란시스코 -> [('시애틀', 678), ('리버사이드', 386), ('로스앤젤레스', 348)]
로스앤젤레스 -> [('샌프란시스코', 348), ('리버사이드', 50), ('피닉스', 357)]
리버사이드 -> [('샌프란시스코', 386), ('로스앤젤레스', 50), ('피닉스', 307), ('시카고', 1704)]
피닉스 -> [('로스앤젤레스', 357), ('리버사이드', 307), ('댈러스', 887), ('휴스턴', 1015)]
시카고 -> [('시애틀', 1737), ('리버사이드', 1704), ('댈러스', 805), ('애틀랜타', 588), ('디트로이트', 238)]
보스턴 -> [('디트로이트', 613), ('뉴욕', 190)]
뉴욕 -> [('디트로이트', 482), ('보스턴', 190), ('필라델피아', 81)]
애틀랜타 -> [('댈러스', 721), ('휴스턴', 702), ('시카고', 588), ('워싱턴', 543), ('마이애미', 604)]
마이애미 -> [('휴스턴', 968), ('애틀랜타', 604), ('워싱턴', 923)]
댈러스 -> [('피닉스', 887), ('시카고', 805), ('애틀랜타', 721), ('휴스턴', 225)]
휴스턴 -> [('피닉스', 1015), ('댈러스', 225), ('애틀랜타', 702), ('마이애미', 968)]
디트로이트 -> [('시카고', 238), ('보스턴', 613), ('워싱턴', 396), ('뉴욕', 482)]
필라델피아 -> [('뉴욕', 81), ('워싱턴', 123)]
워싱턴 -> [('애틀랜타', 543), ('마이애미', 923), ('디트로이트', 396), ('필라델피아', 123)]
프림 알고리즘
프림 알고리즘은 그래프의 모든 정점을 최소 이음선 및 최소 가중치를 사용해 연결하는 방법을 제시한다.
-
최소 이음선
순환 그래프를 비순환적(acyclic)인 신장 트리(spanning tree)로 수정한다. 이음선 가지치기를 통해 사이클(cycle)을 제거할 수 있다.
-
최소 가중치
최소 신장 트리(minimum spanning tree)는 가중치 그래프의 모든 정점을 최소 비용으로 연결한다.
프림 알고리즘은 각 정점에 대해 가장 낮은 가중치를 가진 이음선만을 선택하므로 탐욕적이다.
| 순환 그래프 | 신장 트리 |
|---|---|
 |
 |
priority_queue.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from typing import TypeVar, Generic, List
from heapq import heappush, heappop
T = TypeVar("T")
class PriorityQueue(Generic[T]):
def __init__(self) -> None:
self._container:List[T] = []
@property
def empty(self) -> bool:
return not self._container
def push(self, item:T) -> None:
heappush(self._container, item)
def pop(self) -> T:
return heappop(self._container)
def __repr__(self) -> str:
return repr(self._container)
mst.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from typing import TypeVar, List, Optional
from weighted_graph import WeightedGraph
from weighted_edge import WeightedEdge
from priority_queue import PriorityQueue
V = TypeVar("V") # 그래프 정점(vertice) 타입
WeightedPath = List[WeightedEdge]
def total_weight(wp:WeightedPath) -> float:
return sum([e.weight for e in wp])
def mst(wg:WeightedGraph[V], start:int = 0) -> Optional[WeightedPath]:
"""minimum spanning tree"""
# 시작 정점이 유효하지 않은 경우 None
if start > (wg.vertex_count - 1) or start < 0:
return None
result:WeightedPath = []
pq:PriorityQueue[WeightedEdge] = PriorityQueue()
visited:List[bool] = [False] * wg.vertex_count # 방문한 곳
def visit(index:int):
visited[index] = True
for edge in wg.edges_for_index(index):
if not visited[edge.v]:
pq.push(edge)
visit(start)
while not pq.empty:
edge = pq.pop()
if visited[edge.v]:
continue
result.append(edge)
visit(edge.v)
return result
def print_weighted_path(wg:WeightedGraph, wp:WeightedPath) -> None:
for edge in wp:
print(f"{wg.vertex_at(edge.u)} {edge.weight}> {wg.vertex_at(edge.v)}")
print(f"가중치 총합: {total_weight(wp)}")
-
시작 정점(start)을 최소 신장 트리에 추가한다.
-
현재 정점에 연결된 최소 가중치의 이음선을 찾는다. 이 과정에서 우선순위 큐가 사용된다. 이음선에 연결된 정점을 최소 신장 트리에 추가하며, 이미 추가된 정점이라면 다음 우선순위를 가진 이음선을 탐색한다. 우선순위 큐가 빌 때까지(모든 정점이 최소 신장 트리에 추가될 때까지) 이 과정을 반복한다.
mst.py (계속)
1
2
3
4
5
6
7
if __name__ == "__main__":
...
result:Optional[WeightedPath] = mst(city_graph2)
if result is None:
print("최소 신장 트리로 답을 찾을 수 없습니다!")
else:
print_weighted_path(city_graph2, result)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
시애틀 678> 샌프란시스코
샌프란시스코 348> 로스앤젤레스
로스앤젤레스 50> 리버사이드
리버사이드 307> 피닉스
피닉스 887> 댈러스
댈러스 225> 휴스턴
휴스턴 702> 애틀랜타
애틀랜타 543> 워싱턴
워싱턴 123> 필라델피아
필라델피아 81> 뉴욕
뉴욕 190> 보스턴
워싱턴 396> 디트로이트
디트로이트 238> 시카고
애틀랜타 604> 마이애미
가중치 총합: 5372
Note
n개의 정점을 모두 연결하기 위해 필요한 이음선의 개수는 n-1개이다. 위 문제는 15개의 정점을 사용하므로 그래프의 신장 트리는 14개의 이음선을 가진다. 모든 정점을 연결하는 과정은 14번 이루어지며, 매번 최소 가중치만을 선택하므로 생성되는 신장 트리는 항상 다른 신장 트리보다 작거나 같은 가중치 총합을 가진다. 따라서 프림 알고리즘은 항상 최소 신장 트리를 생성한다.
다익스트라 알고리즘
비가중 그래프의 최단 경로는 너비 우선 탐색을 통해 구할 수 있었다. 가중 그래프의 최단 경로는 이음선의 수가 아닌, 가중치의 합을 기준으로 계산한다. 다익스트라 알고리즘은 그래프의 모든 정점을 최소 이음선 및 최소 가중치를 사용해 연결하는 방법을 제시한다.
다익스트라 알고리즘은 다른 모든 정점으로의 최단 경로(이음선의 모음)와, 그 길이를 반환한다.
dijkstra.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
from __future__ import annotations
from turtle import distance
from typing import TypeVar, List, Optional, Tuple, Dict
from dataclasses import dataclass
from priority_queue import PriorityQueue
from mst import WeightedPath, print_weighted_path
from weighted_graph import WeightedGraph
from weighted_edge import WeightedEdge
from priority_queue import PriorityQueue
V = TypeVar("V") # 그래프 정점(vertice) 타입
@dataclass
class DijkstraNode:
vertex:int
distance:float
def __lt__(self, other:DijkstraNode) -> bool:
return self.distance < other.distance
def __eq__(self, other:DijkstraNode) -> bool:
return self.distance == other.distance
def dijkstra(wg:WeightedGraph[V], root:V) -> Tuple[List[Optional[float]], Dict[int, WeightedEdge]]:
first:int = wg.index_of(root)
distances:List[Optional[float]] = [None] * wg.vertex_count
distances[first] = 0
path_dict:Dict[int, WeightedEdge] = {}
pq:PriorityQueue[DijkstraNode] = PriorityQueue()
pq.push(DijkstraNode(first, 0))
while not pq.empty:
u:int = pq.pop().vertex
dist_u:float = distances[u]
for we in wg.edges_for_index(u):
dist_v:float = distances[we.v]
if dist_v is None or dist_v > we.weight + dist_u:
distances[we.v] = we.weight + dist_u
path_dict[we.v] = we
pq.push(DijkstraNode(we.v, we.weight + dist_u))
return distances, path_dict
def distance_array_to_vertex_dict(wg:WeightedGraph[V], distances:List[Optional[float]]) -> Dict[V, Optional[float]]:
distance_dict:Dict[V, Optional[float]] = {}
for i in range(len(distances)):
distance_dict[wg.vertex_at(i)] = distances[i]
return distance_dict
def path_dict_to_path(start:int, end:int, path_dict:Dict[int, WeightedEdge]) -> WeightedPath:
if len(path_dict) == 0:
return []
edge_path:WeightedPath = []
e:WeightedEdge = path_dict[end]
edge_path.append(e)
while e.u != start:
e = path_dict[e.u]
edge_path.append(e)
return list(reversed(edge_path))
- DijkstraNode는 현재까지 탐색된 정점의 인덱스와 그 거리를 저장한다. 특수 메서들를 사용해 거리를 기준으로 비교하는 기능을 추가한다.
- distances 리스트는 root에서 각 정점까지의 거리를 저장한다.
- root의 DijkstraNode를 우선순위 큐에 push한다.
- 우선순위 큐에서 가장 가까운 정점을 pop한 뒤, 현재 정점(u)으로 설정한다. 이후 현재 정점에 연결된 모든 이음선을 대상으로 탐색을 시도하며, 새로운 최단 경로가 발견될 때마다 거리와 우선순위 큐를 갱신한다. 우선순위 큐가 빌 때까지 이 과정을 반복한다.
dijkstra.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
if __name__ == "__main__":
...
root = "로스앤젤레스"
distances, path_dict = dijkstra(city_graph2, root)
name_distance:Dict[str, Optional[int]] = distance_array_to_vertex_dict(city_graph2, distances)
print(f"{root}에서의 거리:")
for key, value in name_distance.items():
print(f"{key} : {value}")
print("")
goal = "보스턴"
print(f"{root}에서 {goal}까지의 최단 경로:")
path:WeightedPath = path_dict_to_path(city_graph2.index_of(root),
city_graph2.index_of(goal),
path_dict)
print_weighted_path(city_graph2, path)
distance_array_to_vertex_dict는 헬퍼 함수로, 작성한 그래프를 다익스트라 알고리즘의 인자로 변환한다. path_dict_to_path는 반환값을 출력한다(너비 우선 탐색에서 사용했던 node_to_path 함수와 유사).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
로스앤젤레스에서의 거리:
시애틀 : 1026
샌프란시스코 : 348
로스앤젤레스 : 0
리버사이드 : 50
피닉스 : 357
시카고 : 1754
보스턴 : 2605
뉴욕 : 2474
애틀랜타 : 1965
마이애미 : 2340
댈러스 : 1244
휴스턴 : 1372
디트로이트 : 1992
필라델피아 : 2511
워싱턴 : 2388
로스앤젤레스에서 보스턴까지의 최단 경로:
로스앤젤레스 50> 리버사이드
리버사이드 1704> 시카고
시카고 238> 디트로이트
디트로이트 613> 보스턴
가중치 총합: 2605
연습문제
사전 준비
1
2
3
4
5
6
from __future__ import annotations
from typing import TypeVar, List
from edge import Edge
from graph import Graph
V = TypeVar("V") # 그래프 정점(vertice) 타입
가중치를 고려하지 않으므로 Edge와 Graph만으로 충분하다.
📝 4-1
그래프 프레임워크에 에지 및 정점 제거를 위한 메서드를 추가하라.
연습문제 4-1.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class RemovableGraph(Graph[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[Edge]] = [[] for _ in vertices]
def remove_vertex(self, vertex:V) -> None:
target:int = self._vertices.index(vertex)
self._edges[target] = []
self._vertices[target] = None
def remove_edge(self, edge:Edge) -> None:
self._edges[edge.u].remove(edge)
self._edges[edge.v].remove(edge.reversed())
def remove_edge_by_indices(self, u:int, v:int) -> None:
edge:Edge = Edge(u, v)
self.remove_edge(edge)
def remove_edge_by_vertices(self, first:V, second:V) -> None:
u:int = self._vertices.index(first)
v:int = self._vertices.index(second)
self.remove_edge_by_indices(u, v)
def neighbors_for_index(self, index:int) -> List[V]:
return list(filter(lambda x: x, map(self.vertex_at, [e.v for e in self._edges[index]])))
def __repr__(self) -> str:
desc:str = ""
for i in range(self.vertex_count):
if not self.vertex_at(i):
continue
desc += f"{self.vertex_at(i)} -> {self.neighbors_for_index(i)}\n"
return desc
Graph 클래스를 재정의한 RemovableGraph는 정점과 이음선을 제거하는 기능을 추가로 수행한다. 리스트 객체의 append 메서드와 반대로 remove 메서드는 항목을 삭제하며, 이를 사용하면 삭제 기능을 수행하는 메서드를 작성할 수 있다.
연습문제 4-1.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
if __name__ == "__main__":
ex41:RemovableGraph[str] = RemovableGraph(["A", "B", "C"])
ex41.add_edge_by_vertices("A", "B")
ex41.add_edge_by_vertices("B", "C")
ex41.add_edge_by_vertices("C", "A")
print(ex41)
ex41.remove_edge_by_vertices("A", "C")
print(ex41)
ex41.remove_vertex("A")
print(ex41)
1
2
3
4
5
6
7
8
9
10
A -> ['B', 'C']
B -> ['A', 'C']
C -> ['B', 'A']
A -> ['B']
B -> ['A', 'C']
C -> ['B']
B -> ['C']
C -> ['B']
시행착오
1
2
3
4
def remove_vertex(self, vertex:V) -> None:
target:int = self._vertices.index(vertex)
del self._edges[target]
del self._vertices[target]
처음에는 del을 사용해 리스트에서 항목을 제거하는 방식을 시도했지만, neighbors_for_index 메서드를 사용하는 과정에서 list index out of range 오류가 발생했다. 리스트의 크기를 변화시키는 대신, 삭제된 공간을 비워두기로 했다.
1
2
3
4
def remove_vertex(self, vertex:V) -> None:
target:int = self._vertices.index(vertex)
self._edges[target] = []
self._vertices[target] = None
1
2
3
4
...
None -> []
B -> [None, 'C']
C -> ['B']
정상적으로 작동하지만, 별로 보기 좋은 출력 형태는 아니므로 None을 제외하고 출력하게끔 수정한다. 다음과 같이 __repr__ 특수 메서드를 재정의한다.
1
2
3
4
5
6
7
def __repr__(self) -> str:
desc:str = ""
for i in range(self.vertex_count):
if not self.vertex_at(i):
continue
desc += f"{self.vertex_at(i)} -> {self.neighbors_for_index(i)}\n"
return desc
1
2
3
...
B -> [None, 'C']
C -> ['B']
None은 조건문에서 False로 취급된다. 정점이 None인 경우 출력되지 않는다. 하지만 이음선의 도착 정점(v)에 위치한 None이 제거되지 않았다. 이웃 정점을 반환하는 neighbors_for_index 메서드를 재정의해야 한다.
1
2
def neighbors_for_index(self, index:int) -> List[V]:
return list(map(self.vertex_at, filter(lambda x: x, [e.v for e in self._edges[index]])))
filter 함수를 사용해 조건을 제시하고, 부합하는 항목만 리스트에 추가한다. 조건으로 사용되는 함수는 None을 제외한 모든 인자에 대해 True를 반환한다.
1
2
3
4
5
6
7
8
9
10
A -> ['B', 'C']
B -> ['C']
C -> ['B']
A -> ['B']
B -> ['C']
C -> ['B']
B -> ['C']
C -> ['B']
None은 더 이상 보이지 않지만, 출력 결과가 조금 이상하다. 제거할 None은 vertex_at 함수의 반환값인데, 반환값이 아닌 인자에 대해 filter 함수를 수행했기 때문이다. 따라서 filter 함수의 위치를 조정한다.
1
2
def neighbors_for_index(self, index:int) -> List[V]:
return list(filter(lambda x: x, map(self.vertex_at, [e.v for e in self._edges[index]])))
📝 4-2
그래프 프레임워크에 유향 그래프(digraph)를 사용할 수 있도록 코드를 추가하라.
연습문제 4-2.py
1
2
3
4
5
6
7
8
class Digraph(Graph[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[Edge]] = [[] for _ in vertices]
def add_edge(self, edge:Edge) -> None:
self._edges[edge.u].append(edge)
# self._edges[edge.v].append(edge.reversed())
역방향의 이음선을 추가하는 줄만 제거하면 간단하게 해결할 수 있다. 하지만 이렇게 끝내기는 아쉬우니 조금의 기능 개선을 시도해 보자.
1
2
3
4
5
6
7
8
9
10
11
if __name__ == "__main__":
ex42:Digraph[str] = Digraph(["A", "B", "C"])
ex42.add_edge_by_vertices("A", "B")
ex42.add_edge_by_vertices("A", "C")
ex42.add_edge_by_vertices("B", "A")
ex42.add_edge_by_vertices("B", "C")
ex42.add_edge_by_vertices("C", "A")
ex42.add_edge_by_vertices("C", "B")
print(ex42)
Digraph에서는 양방향(무향) 방식이 아닌 단방향(유향) 방식으로 이음선을 추가한다. 하지만 만약 두 정점 A와 B를 연결하는 이음선이 양방향이라면, 두 줄에 걸친 작업을 해야 하므로 상당히 번거롭다. add_edge_by_vertices에 매개변수를 추가해 True일 경우 양방향, False일 경우 단방향으로 이음선을 추가하도록 변경한다면 불필요한 작업을 줄일 수 있을 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Digraph(Graph[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[Edge]] = [[] for _ in vertices]
def add_edge(self, edge:Edge, direction:bool = False) -> None:
self._edges[edge.u].append(edge)
if not direction:
self._edges[edge.v].append(edge.reversed())
def add_edge_by_indices(self, u:int, v:int, direction:bool = False) -> None:
edge:Edge = Edge(u, v)
self.add_edge(edge, direction)
def add_edge_by_vertices(self, first:V, second:V, direction:bool = False) -> None:
u:int = self._vertices.index(first)
v:int = self._vertices.index(second)
self.add_edge_by_indices(u, v, direction)
이음선은 direction 매개변수가 True일 때 단방향, False일 때 양방향 성질을 갖는다.

유향 그래프 클래스를 사용해 위 그림을 정형화한다. A와 C 는 무향으로 연결되어 있지만, B와 A, B와 C에는 오직 하나의 방향만 존재한다.
연습문제 4-2.py (계속)
1
2
3
4
5
6
7
8
if __name__ == "__main__":
ex42:Digraph[str] = Digraph(["A", "B", "C"])
ex42.add_edge_by_vertices("A", "C", False) # 무향
ex42.add_edge_by_vertices("B", "A", True) # 유향
ex42.add_edge_by_vertices("B", "C", True) # 유향
print(ex42)
1
2
3
A -> ['C']
B -> ['A', 'C']
C -> ['A']
📝 4-3
그래프 프레임워크를 사용하여 위키피디아 설명되어 있는 것과 같은 쾨니히스베르크 다리 건너기 문제를 증명 또는 반증하라.

쾨니히스베르크 다리 문제를 정점 A, B, C, D와 이음선a, b, c, d, e, f, g를 갖는 무향 비가중 그래프로 정형화한다. 이 그래프는 특이하게도 두 정점을 연결하는 이음선이 여러 개 존재한다. 예를 들어, A와 B를 연결하는 이음선은 a, b로 두 개 존재한다. 이러한 그래프를 다중 그래프(multigraph)라고 한다. 다중 그래프를 지원하도록 재정의한다.
연습문제 4-3.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
@dataclass
class bridgeEdge(Edge):
id:int # 식별자
def reversed(self) -> bridgeEdge:
return Edge(self.v, self.u, self.id)
def __repr__(self) -> str:
return f"<{self.id}> {self.u} -> {self.v}"
class BridgeGraph(Graph[V]):
def __init__(self, vertices:List[V] = []) -> None:
self._vertices:List[V] = vertices
self._edges:List[List[BridgeEdge]] = [[] for _ in vertices]
def add_edge_by_indices(self, u:int, v:int, name:str) -> None:
edge:BridgeEdge = BridgeEdge(u, v, name)
self.add_edge(edge)
def add_edge_by_vertices(self, first:V, second:V, name:str) -> None:
u:int = self._vertices.index(first)
v:int = self._vertices.index(second)
self.add_edge_by_indices(u, v, name)
이음선을 구분하기 위한 이름 속성을 추가한다.
연습문제 4-3.py (계속)
1
2
3
4
5
6
7
8
9
10
11
12
if __name__ == "__main__":
ex43:BridgeGraph[str] = BridgeGraph(["A", "B", "C", "D"])
ex43.add_edge_by_vertices("A", "B", "a")
ex43.add_edge_by_vertices("A", "B", "b")
ex43.add_edge_by_vertices("A", "C", "c")
ex43.add_edge_by_vertices("A", "C", "d")
ex43.add_edge_by_vertices("A", "D", "e")
ex43.add_edge_by_vertices("B", "D", "f")
ex43.add_edge_by_vertices("C", "D", "g")
print(ex43)
1
2
3
4
A -> ['B', 'B', 'C', 'C', 'D']
B -> ['A', 'A', 'D']
C -> ['A', 'A', 'D']
D -> ['A', 'B', 'C']
재귀를 사용한 백트래킹을 시도한다.
1
2
3
4
5
6
7
8
9
10
if __name__ == "__main__":
ex43:BridgeGraph[str] = BridgeGraph(["A", "B", "C", "D"])
ex43.add_edge_by_vertices("A", "B", "a")
ex43.add_edge_by_vertices("A", "B", "b")
ex43.add_edge_by_vertices("A", "C", "c")
ex43.add_edge_by_vertices("A", "C", "d")
ex43.add_edge_by_vertices("A", "D", "e")
ex43.add_edge_by_vertices("B", "D", "f")
ex43.add_edge_by_vertices("C", "D", "g")
print(ex43)
쾨니히스베르크 다리 문제를 프레임워크에 입력한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
...
def visit(current:BridgeEdge, explored:List[BridgeEdge]):
# 종료 조건: 모든 다리를 한 번씩 건넌다.
if len(explored) == (ex43.edge_count / 2):
print(explored) # 출력
exit() # 종료
# 이동 가능한 곳
promise:List[BridgeEdge] = list(filter(lambda x: False if (x.name in current.name) else True,
ex43.edges_by_edge(current)))
print(f"-----{current}-------------------------")
print(f"이미 지난 곳: {explored}")
print(f"이동 가능한 곳: {promise}")
# promise의 모든 BridgeEdge에 대한 탐색 시행
for edge in promise:
# 건널 수 없으면 continue
if edge.name in explored:
print(f"{edge.name} -> 불가능", end=" ")
continue
# 건널 수 있으면 재귀
print(f"{edge.name} -> 가능")
print(f"{edge.name}로 이동합니다.")
print("\n\n")
explored.append(edge.name)
visit(edge, explored)
# promise가 존재하지 않으면 되추적
explored.remove(current.name)
print()
promise는 현재 다리의 끝 정점에서 건널 수 있는 다리의 리스트를 반환한다.
explored는 이미 건넌 다리의 이름을 저장한다. 이 리스트의 항목은 탐색의 제외 대상이 된다.
1
2
3
4
5
...
initial = ex43._edges[1][0]
explored:List[str] = [initial.name]
visit(initial, explored)
print("실패!") # 출력
종료 조건을 만족하면 결과(다리의 이름이며, 이 순서대로 건너면 된다)를 출력한다. -> 가능하다.
모든 호출이 실행되고 함수가 종료되면 실패 메세지를 출력한다. -> 불가능하다.
1
2
3
4
5
6
7
8
9
-----<c> 0 -> 2-------------------------
이미 지난 곳: ['a', 'e', 'g', 'd', 'c']
이동 가능한 곳: [<d> 2 -> 0, <g> 2 -> 3]
d -> 불가능 g -> 불가능
e -> 불가능
실패!
따라서 쾨니히스베르크 다리 문제는 해결할 수 없다.
경로 추가
A와 D 사이에 다리를 하나 더 놓으면 모든 다리를 한 번씩 건널 수 있다.
1
2
3
4
5
6
7
8
9
10
11
if __name__ == "__main__":
ex43:BridgeGraph[str] = BridgeGraph(["A", "B", "C", "D"])
ex43.add_edge_by_vertices("A", "B", "a")
ex43.add_edge_by_vertices("A", "B", "b")
ex43.add_edge_by_vertices("A", "C", "c")
ex43.add_edge_by_vertices("A", "C", "d")
ex43.add_edge_by_vertices("A", "D", "e")
ex43.add_edge_by_vertices("B", "D", "f")
ex43.add_edge_by_vertices("C", "D", "g")
ex43.add_edge_by_vertices("A", "D", "h") # 추가된 경로
print(ex43)
아래는 새로운 경로를 추가한 뒤 <a> 1 -> 0 다리에서 시작했을 때의 과정 및 결과(성공)를 나타낸 것이다. 한붓그리기 문제의 경우 모든 조건이 성공으로 이어지는 것은 아니다. 만약 실패한다면 시작 정점과 이음선을 다르게 설정해야 한다(for문을 사용하면 모든 조건에 대해 한 번에 탐색 가능).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
-----<a> 1 -> 0-------------------------
이미 지난 곳: ['a']
이동 가능한 곳: [<b> 0 -> 1, <c> 0 -> 2, <d> 0 -> 2, <e> 0 -> 3, <h> 0 -> 3]
b -> 가능
b로 이동합니다.
-----<b> 0 -> 1-------------------------
이미 지난 곳: ['a', 'b']
이동 가능한 곳: [<a> 1 -> 0, <f> 1 -> 3]
a -> 불가능 f -> 가능
f로 이동합니다.
-----<f> 1 -> 3-------------------------
이미 지난 곳: ['a', 'b', 'f']
이동 가능한 곳: [<e> 3 -> 0, <g> 3 -> 2, <h> 3 -> 0]
e -> 가능
e로 이동합니다.
-----<e> 3 -> 0-------------------------
이미 지난 곳: ['a', 'b', 'f', 'e']
이동 가능한 곳: [<a> 0 -> 1, <b> 0 -> 1, <c> 0 -> 2, <d> 0 -> 2, <h> 0 -> 3]
a -> 불가능 b -> 불가능 c -> 가능
c로 이동합니다.
-----<c> 0 -> 2-------------------------
이미 지난 곳: ['a', 'b', 'f', 'e', 'c']
이동 가능한 곳: [<d> 2 -> 0, <g> 2 -> 3]
d -> 가능
d로 이동합니다.
-----<d> 2 -> 0-------------------------
이미 지난 곳: ['a', 'b', 'f', 'e', 'c', 'd']
이동 가능한 곳: [<a> 0 -> 1, <b> 0 -> 1, <c> 0 -> 2, <e> 0 -> 3, <h> 0 -> 3]
a -> 불가능 b -> 불가능 c -> 불가능 e -> 불가능 h -> 가능
h로 이동합니다.
-----<h> 0 -> 3-------------------------
이미 지난 곳: ['a', 'b', 'f', 'e', 'c', 'd', 'h']
이동 가능한 곳: [<e> 3 -> 0, <f> 3 -> 1, <g> 3 -> 2]
e -> 불가능 f -> 불가능 g -> 가능
g로 이동합니다.
['a', 'b', 'f', 'e', 'c', 'd', 'h', 'g']
Note
연결된 이음선의 개수가 홀수인 정점을 홀수점, 그렇지 않은 정점을 짝수점이라고 한다. 한붓그리기 문제는 홀수점의 개수에 따라 해결 여부가 달라진다.
홀수점의 개수 해결 여부 0 가능(어느 점에서 출발해도 무관) 2 가능(홀수점 -> 다른 홀수점) 4 이상 불가능