• 버블 정렬
• 개선 알고리즘
  • 조기 종료
  • 조기 종료++
• 요약

버블 정렬

1
2
3
4
5
6
def bubble_sort(arr):
    n = len(arr)
    for i in range(n-1):
        for j in range(n-1, i, -1):
            if arr[j-1] > arr[j]:
                arr[j-1], arr[j] = arr[j], arr[j-1]

• 비교

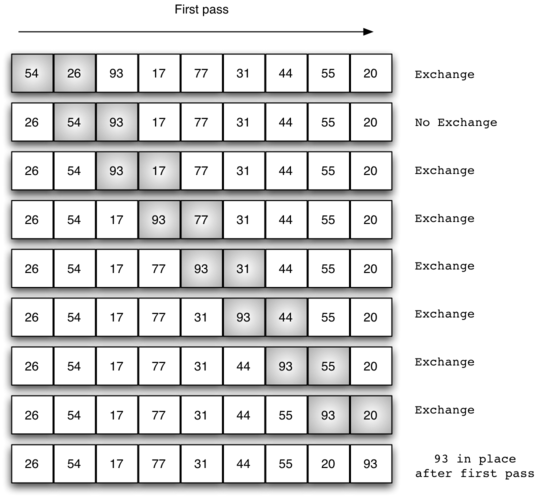
  인접한 두 요소를 비교한다. n개의 요소를 정렬할 때 첫 번째 패스(pass)에서는 n-1번의 비교가 이루어지며, 모든 비교 과정이 끝나면 다음 패스로 넘어간다. 패스의 비교 횟수가 1이 될 때까지 비교하므로 총 n(n-1)/2번 비교한다.

• 교환

  조건을 만족하면 교환한다. 왼쪽 인덱스의 값이 오른쪽 인덱스의 값보다 크다면 두 요소를 교환하며, 패스가 끝날 때마다 최대값이 가장 오른쪽으로 밀려난다. 역순으로 정렬되어 있는 경우 모든 비교에 대해 교환이 이루어지므로 최대 n(n-1)/2번 교환한다.

개선 알고리즘

조기 종료

하나의 패스에서 교환이 한 번도 발생하지 않았다면, 리스트가 정렬이 완료되었음을 의미한다. 이를 바탕으로 종료 조건을 추가해 알고리즘을 개선할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
def bubble_sort_2(arr):
    n = len(arr)
    for i in range(n-1):
        exchanges = False
        for j in range(n-1, i, -1):
            if arr[j-1] > arr[j]:
                exchanges = True
                arr[j-1], arr[j] = arr[j], arr[j-1]

        if not exchanges:
            break

조기 종료++

1

요약

O(n ^ 2)의 높은 시간 복잡도를 가지고 있으며, 모든 반복에 대해 비교와 교환이 이루어질 수 있다.

버블 정렬은 같은 시간복잡도를 가진 다른 알고리즘(선택 정렬, 삽입 정렬)에 비해서도 낮은 효율을 보여준다.

그러나 안정적인 교환(stable)이 이루어지고 조기 종료를 통해 시간을 단축할 수 있다.