정지 문제(Halting problem)
알고리즘은 주어진 문제를 해결하기 위한 절차나 방법을 의미한다.
아래 영상에서는 알고리즘으로 해결할 수 없는 문제인 정지 문제에 대해서 소개한다.
완벽한 기계
machine_A는 주어진 연산 문제를 완벽하게 해결하는 알고리즘이다.
이 문서에서 소개하는 machine들을 구현하기 위한 알고리즘은 간단히 추상화하였다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def machine_A (num_a, num_b, operator):
if operator == "+":
return num_a + num_b;
if operator == "-":
return num_a - num_b;
if operator == "*":
return num_a * num_b;
if operator == "/":
return num_a / num_b;
else:
pass
if __name__ == "__main__":
machine_A (3, 5, "+")
1
8
machine_C는 체커판의 현재 상태가 주어지면 최적의 수를 출력하는 알고리즘이다.
이 알고리즘은 체커판의 배열을 입력받아 플레이어가 취할 수 있는 최적의 수를 출력한다.
(알고리즘이 복잡한 관계로 이 문서에서는 print 함수를 대신 사용해 간단하게 표현)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
def machine_C (pieces):
print("Do the best play in player's turn")
# 0 is blank, 1 is player1, 2 is player 2
pieces = np.array([
[0, 1, 0, 1, 0, 1, 0, 1, 0, 1],
[1, 0, 1, 0, 1, 0, 1, 0, 1, 0],
[0, 1, 0, 1, 0, 1, 0, 1, 0, 1],
[1, 0, 1, 0, 1, 0, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 2, 0, 2, 0, 2, 0, 2, 0, 2],
[2, 0, 2, 0, 2, 0, 2, 0, 2, 0],
[0, 2, 0, 2, 0, 2, 0, 2, 0, 2],
[2, 0, 2, 0, 2, 0, 2, 0, 2, 0]
])
if __name__ == "__main__":
machine_C (pieces)
1
Do the best play in player's turn
문제 발생
machine_A는 연산 영역에서 완벽해 보인다.
하지만 machine_A에 체커판의 배열을 입력한다면 문제가 발생한다.
1
machine_A (pieces)
1
2
3
4
5
6
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-13-923d387e2ab2> in <module>
----> 1 machine_A (pieces)
TypeError: machine_A() missing 2 required positional arguments: 'num_b' and 'operator'
그 이유는 machine_A가 이러한 입력을 처리하도록 설계되지 않았기 때문이다.
따라서 체커판의 배열을 입력한다면 machine_A의 작동은 멈춰(Stuck)버린다.
machine_C에 연산식을 입력해도 같은 문제가 발생한다.
1
machine_C (3, 5, "+")
1
2
3
4
5
6
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-15-a5cc8fa42fed> in <module>
----> 1 machine_C (3, 5, "+")
TypeError: machine_C() takes 1 positional argument but 3 were given
정지 정리
machine_H
정지 문제를 검토하는 알고리즘 machine_H (P, I)이 있다고 가정하자.
machine_H는 두 개의 값을 입력받는다. P에 테스트할 알고리즘을, I에 그 알고리즘에 필요한 입력값을 대입하면, machine_H는 그 알고리즘이 멈추지 않을지 결정한다.
예를 들어 P에 machine_A를, I에 [3, 2, “+”]를 입력하는 상황을 가정해 보자. machine_A (3, 2, "+")는 정상적으로 5를 반환할 것이다.
즉 machine_A 알고리즘은 멈추지 않으므로 machine_H는 True를 출력한다.
machine_X
machine_H의 존재 여부를 증명하기 위해서, 2개의 machine을 추가로 생성한다.
machine_P는 값을 입력받으면, 입력받은 값의 두 복사본을 리스트에 담아 반환한다.
1
2
3
4
5
6
7
def machine_P (x):
return x, x
if __name__ == "__main__":
machine_P(2)
print(machine_P(2)[0])
print(machine_P(2)[1])
1
2
2
2
machine_N은 True를 입력받으면 False를, False를 입력받으면 True를 리턴한다.
1
2
3
4
5
6
7
8
9
def machine_N (x):
if x == True:
return False
if x == False:
return True
if __name__ == "__main__":
print(machine_N(True))
print(machine_N(False))
1
2
False
True
3개의 machine을 연결한 뒤, 연결된 machine을 machine_X라고 하자.
machine_X는 machine_H, machine_P, machine_N이 순차적으로 연결되어 있다.
machine_X의 입력값에 machine_H를 대입한다.
1
2
3
result_N1, result_N2 = machine_N (machine_H)
result_H = machine_H (result_N1, result_N2) # machine_H (machine_H, machine_H)
result_N = machine_N (result_H)
| machine_P의 결과 | muchine_H의 알고리즘 | machine_H의 결과 | machine_N의 결과 | 가정 결과 |
|---|---|---|---|---|
| machine_H, machine_H | machine_X가 True를 반환한다고 가정 | True | False | 가정과 다른 결과 |
| machine_H, machine_H | machine_X가 False를 반환한다고 가정 | False | True | 가정과 다른 결과 |
증명
machine_A나 machine_C가 그랬던 것처럼, machine_H 또한 항상 완벽하게 작동해야만 한다.
하지만 machine_X를 사용하면 machine_H가 잘못된 결과를 출력하는 경우를 찾아낼 수 있다.
따라서 귀류법에 의해 전제에 machine_H는 존재 할 수 없다.
Note machine_H의 존재 여부를 증명하는 데 사용된 방법을 귀류법이라고 한다. 귀류법의 과정을 요약하면 다음과 같다.
- machine_H가 존재한다고 가정한다.
- machine_H가 잘못된 결과를 출력하는 경우를 찾아낸다.
- 이 때 잘못된 결과를 출력한다면, 전제에 모순되기 때문에 machine_H는 존재할 수 없다.
엄밀한 증명
Turing Machine[1]을 통해 정지 문제를 증명할 수 있다.
Turing Machine은 다른 Turing Machine과 문자열을 입력받는 알고리즘이다.
Halting machine은 다음과 같이 작동하는 Turing Machine(이하 HM_1)이다.
- 입력받은 튜링 머신(이하 H)의 연산이 유한한 시간 내에 완료되면 HM_1은 Yes를 반환한다.
- H의 연산이 유한한 시간 내에 완료되지 않으면 HM_1은 No를 반환한다.
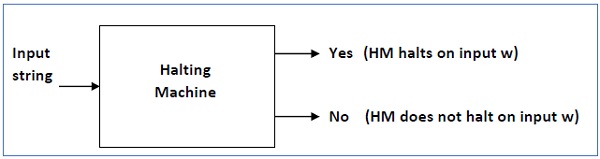
inverted halting machine은 다음과 같이 동작하는 Turing Machine(이하 HM_2)이다.
- H의 연산이 Yes를 반환하면 HM_2는 무한 루프한다.
- H의 연산이 No를 반환하면 HM_2는 중지한다.
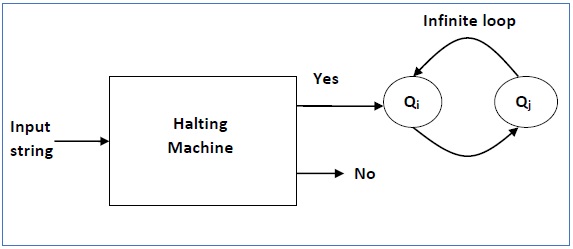
이제 두 Turing Machine을 서로 연결해 새로운 Turing Machine(이하 HM_3)을 만든다.
이제 HM_1의 반환값을 통해 정지 문제의 결정 여부를 증명한다.
- 만약 HM_1이 Yes를 반환한다면
- HM_2는 무한 루프할 것이다.
- 따라서, HM_1은 No를 반환할 것이다.
- 즉, 전제에 모순된다.
-
만약 HM_1이 No를 반환한다면
-
HM_2는 중지할 것이다.
-
따라서, HM_1은 Yes를 반환할 것이다.
-
즉, 전제에 모순된다.
-
어떤 값을 반환하는지에 관계없이 반환값은 전제에 모순된다. 따라서 정지 문제는 결정할 수 없다.
결론
지금까지 정지 문제가 알고리즘으로 해결할 수 없다는 것을 증명했다. 알고리즘이 만능 열쇠는 아니라는 다른 대표적인 예시로 난수 생성을 들 수 있다. 난수 생성은 시스템 시간 등을 사용해 시드(Seed)를 생성하는 방식으로 작동하며, 얼핏 보면 완벽한 무작위처럼 보인다. 하지만 이러한 방식은 유추가 가능한 방식이기에 완전하다고 단언할 수는 없다. 그렇기 때문에 컴퓨터가 생성한 난수를 의사 난수라고 부른다. 반면 인간이 생각하는 무작위 수는 예측할 수 없다. 그렇기에 칠판에 적힌 문제를 풀 학생을 정하는 선생님의 난수 생성 방식은 어떠한 알고리즘으로도 예측할 수 없다(최근 들어서 난수 생성의 난관은 양자 난수 등의 기술을 적용한 하드웨어와의 결합으로 극복되고 있다).
machine_H를 만드는 것은 어쩌면 가능하지 않을까? 알파고가 그랬던 것처럼, machine_H를 수많은 데이터와 이를 기반으로 한 학습을 바탕으로 구현한다면 어떤 알고리즘의 청사진이든(심지어 자기 자신까지도) 결과를 예상할 수 있지 않을까? 그러나 이것은 모순이다. machine_X에 machine_H의 청사진을 입력하면, 그 안의 machine_H는 항상 잘못된 값을 가정하는 무한 루프에 빠지게 된다. machine_H의 무한 루프를 검토하는 다른 알고리즘을 만든다고 해도, 그 알고리즘이 정확히 판별할 수 없는 함수가 적어도 하나 존재하게 된다.
인간의 사고 또한 무한 루프에 가로막혀 답을 낼 수 없는 경우가 존재한다. 단적인 예시로 ‘창조주의 창조주는 누구인가?’라는 물음은 꼬리에 꼬리를 물고 이어진다. 사람들은 이에 대해 저마다의 답을 내놓는다. 그렇지만 정지 문제를 해결할 수 있는 알고리즘이 없듯이, 이 물음에 대해 논리적 증명을 할 수 있는 사람은 없다. 사람과 컴퓨터는 미제를 공유하는 사이다. 어쩌면 이러한 공통점이 프로그래밍에 끌리는 이유인지도 모른다.
- “컴퓨터가 모든 것을 해결할 수 없다는 증명 (정지 문제)”, udiprod 유튜브, Link (2021.10.04)
- “정지 문제”, 기계인간 깃허브 블로그, Link (2021.10.04)